【導(dǎo)讀】對于在反饋環(huán)路中采用MEMS慣性測量單元(IMU)的高性能運動控制系統(tǒng),傳感器對準誤差常常是其關(guān)鍵考慮之一。對于IMU中的陀螺儀,傳感器對準誤差描述各陀螺儀的旋轉(zhuǎn)軸與系統(tǒng)定義的“慣性參考系”(也稱為“全局坐標系”)之間的角度差。為了管控對準誤差對傳感器精度的影響,可能需要獨特的封裝、特殊的組裝工藝,甚至在最終配置中進行復(fù)雜的慣性測試。
所有這些事情都可能會對項目管理的重要指標:如計劃、投資和各系統(tǒng)中IMU相關(guān)的總成本等,產(chǎn)生重大影響。因此,在設(shè)計周期的早期,當還有時間界定系統(tǒng)架構(gòu)以實現(xiàn)最有效解決方案的時候,對傳感器對準誤差加以考慮是十分有必要的。畢竟,沒有人希望在燒掉項目80%的計劃時間和預(yù)算之后才發(fā)現(xiàn),為了滿足最終用戶不容商量的交貨要求,其并不昂貴的傳感器需要增加數(shù)百甚至數(shù)千美元的意外成本,那樣可就糟糕至極了!
設(shè)計系統(tǒng)的IMU功能架構(gòu)時,有三個基本對準概念需要了解和評估:誤差估計、對準誤差對系統(tǒng)關(guān)鍵行為的影響以及電子對準(安裝后)。初始誤差估計應(yīng)當包括IMU以及在運行過程中將其固定就位的機械系統(tǒng)這兩方面的誤差貢獻。了解這些誤差對系統(tǒng)關(guān)鍵功能的影響有助于確立相關(guān)性能目標,防止過度處理問題,同時管控無法兌現(xiàn)關(guān)鍵性能和成本承諾的風險。最后,為了優(yōu)化系統(tǒng)的性能或以成本換空間,可能需要某種形式的電子對準。
預(yù)測安裝后的對準誤差
一個應(yīng)用的對準精度取決于兩個關(guān)鍵因素:IMU的對準誤差和在運行過程中將其固定就位的機械系統(tǒng)的精度。IMU的貢獻(ΨIMU)和系統(tǒng)的貢獻(ΨSYS)通常并不相關(guān),估計總對準誤差時,常常是利用和方根計算將這兩個誤差源加以合并:
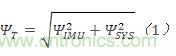
某些IMU規(guī)格表通過“軸到封裝對準誤差”或“軸到坐標系對準誤差”等參數(shù)來量化對準誤差。圖1以夸張方式顯示了ADIS16485中各陀螺儀相對于其封裝邊緣的對準誤差。圖中的綠色虛線代表封裝定義的參考系的各軸。實線代表封裝內(nèi)部陀螺儀的旋轉(zhuǎn)軸,ΨIMU代表三個對準誤差項的最大值(ΨX、ΨY、ΨZ)。
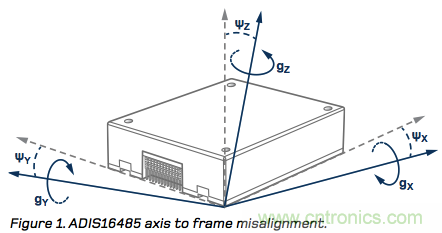
圖1: ADI16485軸到坐標系的對準誤差。
為了預(yù)測系統(tǒng)對準誤差的貢獻(公式1中的ΨSYS),需要分析機械缺陷導(dǎo)致IMU在系統(tǒng)中的停靠位置相對于全局坐標系偏斜的可能性。使用焊接到印刷電路板的IMU時,這將涉及到以下考量因素:原始放置精度、焊料沉積的差異、回流焊期間的浮動、PCB關(guān)鍵特性(如安裝孔等)的容差以及系統(tǒng)框架本身的容差等。使用模塊式IMU時,它可以與系統(tǒng)外殼實現(xiàn)更直接的耦合,如圖2所示。此類接口有兩個關(guān)鍵機械特性可幫助管控安裝偏斜誤差:安裝架(4×)和安裝巢。
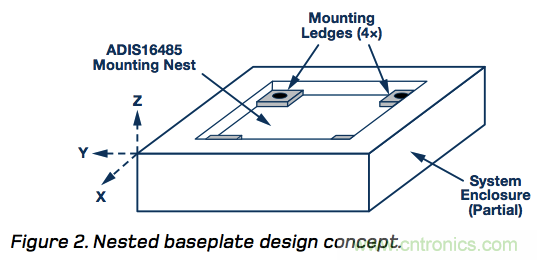
圖2:內(nèi)嵌式底板設(shè)計概念。
在此類安裝方案中,四個安裝架的高度差異就是機械差異的一個例子,可能引起x軸和y軸的安裝偏斜。圖3以夸張方式說明了這種偏差(H1與H2)對x軸安裝偏斜(ΨX)的影響。
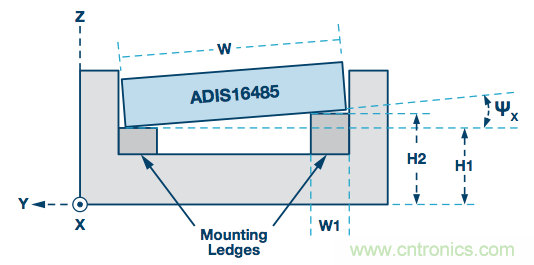
圖3:安裝架差異引起的對準誤差。
Mounting Ledges: 安裝架
公式2反映了x軸偏斜角度(ΨX)與高度差(H2到H1)和兩個接觸點間跨度(W到W1)的關(guān)系:
安裝架高度差異對y軸的安裝偏斜也有類似的影響。此時,?用封裝長度(L)替換公式2中的寬度(W),便可得到如下用于估計y軸偏斜角度(ΨY)的關(guān)系式。
圖4提供了另一個例子來說明機械特性如何影響z軸的安裝偏斜。本例中,機械螺絲先穿過IMU主體的安裝孔(位于四角),再穿過安裝架的孔,最后進入安裝架背部的鎖緊螺母。這種情況下,機械螺絲的直徑(DM)與底板中相關(guān)通孔的直徑(DH)之間的差異會引起z軸偏斜。
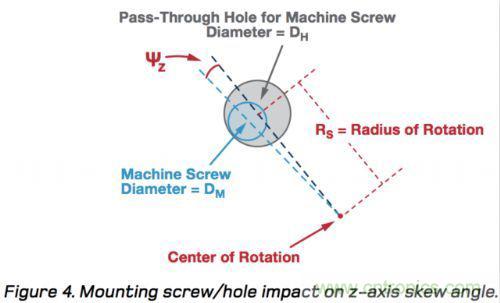
圖4:安裝螺絲/孔對z軸偏斜角度的影響。
公式4反映了z軸安裝偏斜(ΨZ)與直徑差和旋轉(zhuǎn)半徑(RS,等于相對兩角的兩個安裝螺絲間距離的一半)的關(guān)系。
7
示例1
使用2mm機械螺絲將ADIS16485安裝到6mm×6mm安裝架上,安裝架的孔直徑為2.85mm,高度容差為0.2mm,估算與此相關(guān)的總對準誤差。
求解
使用44mm的標稱寬度(W),x軸偏斜角度(見圖3)預(yù)測值為0.3度。
封裝各邊上安裝孔間的標稱距離分別為39.6mm和42.6mm。這些尺寸構(gòu)成直角三角形的兩邊,其斜邊等于封裝相對兩角的兩個孔之間的距離。旋轉(zhuǎn)半徑
(RS,見圖4)等于此距離的一半(29.1mm),因此z軸偏斜的預(yù)測值為0.83度。
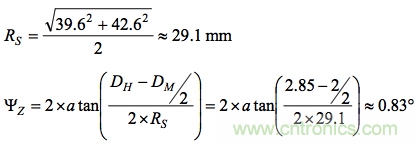
對于式1中的復(fù)合預(yù)測公式,ΨSYS等于ΨZ(估算最大值),ΨIMU等于1度(依據(jù)IMU數(shù)據(jù)手冊中的軸到坐標系對準誤差規(guī)格)。因此,總對準誤差估算值為1.28度。
對準誤差對系統(tǒng)精度的影響
為應(yīng)用制定精度標準時,了解對準誤差與其對陀螺儀精度影響之間的基本關(guān)系是一個很好的著手點。為了說明該過程,圖5提供了三軸陀螺儀系統(tǒng)的通用模型。圖中的三條綠色實線代表全局坐標系的三軸,黑色實線代表所有三個陀螺儀的旋轉(zhuǎn)軸,帶Ψ標簽代表全局坐標系與陀螺儀軸之間的對準誤差。公式5、公式6和公式7顯示了對準誤差對各陀螺儀繞全局坐標系中指定軸旋轉(zhuǎn)的響應(yīng)的影響。在這些公式中,對準角度誤差的余弦引入一個比例誤差。
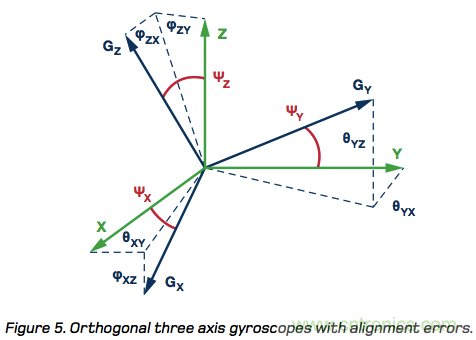
圖5:正交三軸陀螺儀的對準誤差。
對準誤差還會對各軸產(chǎn)生跨軸影響。為了量化這些影響,需要將各軸的對準角度誤差分解為與其它兩軸相關(guān)的兩個分量。例如,ΨX有一個y軸分量(φXY)和一個z軸分量(φXZ),導(dǎo)致x軸陀螺儀對繞全局坐標系中所有三軸旋轉(zhuǎn)(ωX, ωY, ωZ)的響應(yīng)擴展如下:
y軸和z軸陀螺儀也有同樣的擴展:
對公式8、公式9和公式10的兩側(cè)積分,可得到關(guān)于角位移的類似關(guān)系。在得到的公式11、公式12和公式13中,我們關(guān)心的角度是相對于全局坐標系的角位移(θXω, θYω, θZω)和各陀螺儀的積分(θXG, θYG, θZG)。
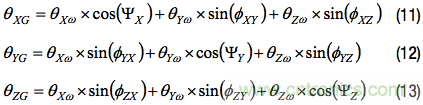
示例2
一種地面無人駕駛車輛(UV)利用MEMS IMU作為平臺穩(wěn)定控制(PSC)系統(tǒng)中的反饋傳感器以支持其天線。此系統(tǒng)采用RSS調(diào)諧器環(huán)路,后者要求方位角和仰角保持在±1?范圍內(nèi),以便維持連續(xù)通信。在大多數(shù)動態(tài)情況下,PSC高度依賴y軸陀螺儀測量來控制仰角,以及依賴z軸陀螺儀測量來控制方位角。在此類動態(tài)情況下,航向角(θZω)的最大變化為30?,并且在作這種機動期間沒有繞x軸或y軸的旋轉(zhuǎn)(θXω = θYω = 0)。
求解
由于繞x軸和y軸的旋轉(zhuǎn)為0,公式8和公式9可簡化為:
從y軸開始,設(shè)θYG的最大邊界為1?,求解對準誤差項ΦYZ。這樣便可求得y軸陀螺儀的最大允許對準誤差為1.9度。
對于z軸,設(shè)θZω等于30?,θZG和θZω之差的最大邊界為1度,然后求解ΨZ。這樣便可求得z軸陀螺儀的最大允許對準誤差為14.8度。
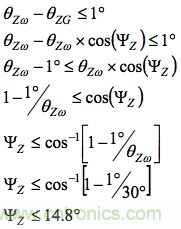
上述計算表明,對于這種特定機動/情形,y軸和z軸之間的跨軸行為要求對準精度約為1.9度。
電子對準
在IMU和安裝系統(tǒng)不滿足關(guān)鍵系統(tǒng)目標的情況下,電子對準提供了一種減小對準誤差的方法。該過程有兩個重要步驟:測定對準誤差項(IMU安裝之后)和制定一個校正對準矩陣。將該矩陣應(yīng)用于陀螺儀陣列時,陀螺儀將像已與全局坐標系對準一樣作出響應(yīng)。公式14為此過程提供了一個系統(tǒng)模型,其中繞全局坐標系各軸的旋轉(zhuǎn)(ω)是三個系統(tǒng)輸入,三個陀螺儀響應(yīng)(G)是系統(tǒng)輸出,3 × 3矩陣(M)代表輸入與輸出之間的系統(tǒng)行為(包括對準誤差)。
通過簡單的算術(shù)操作可得,陀螺儀測量結(jié)果(G)與M的逆矩陣(M–1)的乘積等于全局坐標系的旋轉(zhuǎn)陣列(ω)。因此,對準矩陣等于M–1。
基于公式8、公式9和公式10,可將公式14擴展以包括對準誤差項,如公式16所示,公式17和公式18是更一般形式:
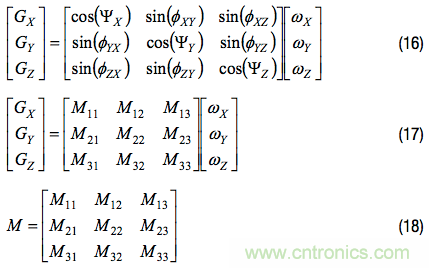
一次僅繞一個軸旋轉(zhuǎn)整個系統(tǒng)可將系統(tǒng)模型簡化到足夠簡單的程度,使得矩陣中的每個元素都可以通過一次陀螺儀測量獲得。例如,讓系統(tǒng)繞x軸旋轉(zhuǎn)(ωX = ωTR, ωY = 0, ωZ = 0),同時觀測所有三個軸,則M11、M21和M31的關(guān)系可簡化如下:
采用同樣的方法,繞y軸旋轉(zhuǎn)(ωX = 0, ωY = ωTR, ωZ = 0),則M12、M22和M32的關(guān)系可簡化如下:

最后,繞z軸旋轉(zhuǎn)(ωX = 0, ωY = 0, ωZ = ωTR),則M13、M23和M33的關(guān)系可簡化如下:

顯然,運動配置(ω)的精度和陀螺儀測量(G)對此過程有直接影響。具體說來,偏軸運動對此過程有顯著影響,當購買和部署依賴這些要求的慣性測試設(shè)備時,必須予以考慮。就陀螺儀精度而言,偏置和噪聲是兩大威脅,在此過程中通常需要考慮。為了管控陀螺儀測量中殘余偏置誤差(bE)的影響,有一個技巧是使用兩個不同的旋轉(zhuǎn)速率——大小相等但方向相反。例如,繞y軸沿正方向旋轉(zhuǎn)時(ωY = ωTR, ωX = ωZ = 0),公式28描述了z軸陀螺儀響應(yīng)和偏置誤差。公式29則描述了繞y軸沿負方向旋轉(zhuǎn)時(ωY = –ωTR, ωX = ωZ = 0)z軸陀螺儀的響應(yīng)。
變換公式29,寫出偏置誤差(bE)的表示形式,代入公式28中,然后求解M32。注意偏置誤差(bE)是如何從公式中消除的。
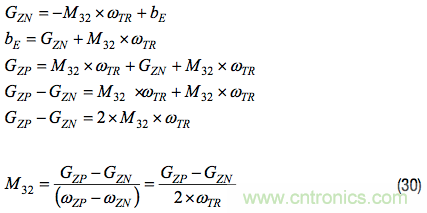
此公式假設(shè)偏置誤差在兩次測量中保持不變,這并不是一個符合實際的期望,不同測量之間可能存在偏差(溫度、時間和噪聲),對此應(yīng)有清醒的認識。當在穩(wěn)定的溫度條件下連續(xù)進行測量時,噪聲常常是此過程中需要管控的關(guān)鍵誤差。在陀螺儀測量中,可接受的噪聲水平取決于對準精度目標(ΨT)和測定過程中各軸上的旋轉(zhuǎn)速率(ωTR)。慣性條件保持不變時,一種常用的降噪技術(shù)是對陀螺儀數(shù)據(jù)求均值。利用Allan方差曲線這個工具可以了解可重復(fù)性(噪聲)與均值時間之間的權(quán)衡關(guān)系。
示例3
如果特性測定期間的旋轉(zhuǎn)速率為100?/s,對準精度目標為0.1度,噪聲(rms)必須比對準誤差目標低10倍,那么為了實現(xiàn)這些目標,我們需要對ADIS16485的輸出求多長時間的均值?
求解
使用陀螺儀與輸入之間的一般響應(yīng)(在測試平臺上旋轉(zhuǎn)),下面的計算表明:各陀螺儀的總噪聲(rms)必須低于62?/小時。
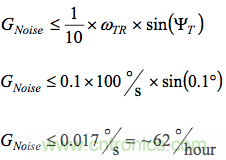
圖6通過一個例子說明了如何使用此IMU的Allan方差曲線來選擇均值時間以滿足上述要求。本例中,0.1秒的均值時間可滿足62?/小時的可重復(fù)性目標,還有一些裕量。
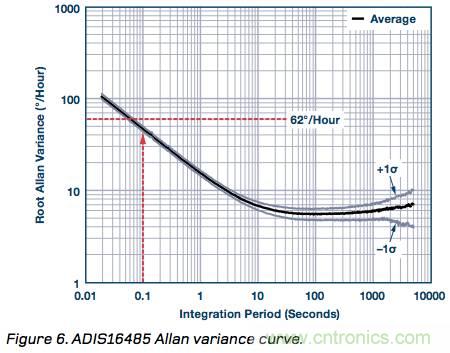
圖6:ADIS16485 Allan方差曲線。
注意,這種方法僅針對傳感器本身的噪聲。若測試平臺有振動,會增加陀螺儀測量的噪聲,則可能需要額外的考慮和濾波。
簡化對準過程的技巧和竅門
開發(fā)一個具有必要的精度和環(huán)境控制溫度的三軸慣性測試系統(tǒng),通常需要在固定設(shè)備和工程開發(fā)資源方面投入巨資。對于那些正在開發(fā)第一代或第二代系統(tǒng),在開發(fā)過程中有很多問題需要回答的公司,可能沒有此類資源或時間。這就產(chǎn)生了簡化解決方案的需求,通過謹慎選擇IMU并利用儀器或應(yīng)用中的自然運動可以實現(xiàn)簡化。
例如,有時候使用角度可能比使用角速率測量來得更方便。公式31是公式11、公式12和公式13合并的結(jié)果,它用相對于全局坐標系的角度(θXω, θYω, θZω)和陀螺儀輸出的積分(θXG, θYG, θZG)來代表系統(tǒng)行為(M):
關(guān)于器件選擇,軸到軸對準誤差是一個需要考慮的重要參數(shù),因為當它低于軸到封裝對準誤差參數(shù)時,將有助于降低與電子對準相關(guān)的慣性測試配置(公式16)的復(fù)雜度。軸到封裝對準誤差參數(shù)描述的是陀螺儀相對于外部機械基準的方位,而軸到軸對準誤差參數(shù)描述的是各陀螺儀相對于另外兩個陀螺儀的方位。多數(shù)情況下,MEMS IMU中三個陀螺儀的理想方位是彼此成90?,因此軸到軸對準誤差與此行為的另一個常見參數(shù)(跨軸靈敏度)相關(guān)。利用公式7作為參考,軸到軸對準誤差代表這三個關(guān)系的最大值:

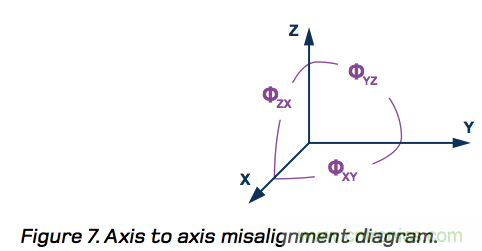
圖7:軸到軸對準誤差。
制定電子對準流程時,軸到軸對準誤差參數(shù)確定的是假設(shè)傳感器完全正交對準時的誤差。使用完全正交這一假設(shè)條件,僅旋轉(zhuǎn)兩軸便可對準所有三軸。例如,繞y軸和z軸旋轉(zhuǎn)便可直接觀測到M12 、M13、M22、M23、M32和M33。假設(shè)完全正交對準并應(yīng)用三角函數(shù),便可利用以上6個元素和以下關(guān)系式計算其他三個元素(M11、M21和M31):
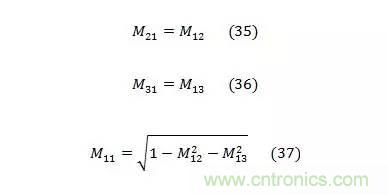
以上等式可將系統(tǒng)模型更新如下,其中M矩陣中的所有9個元素用從y軸和z軸旋轉(zhuǎn)得來的6個元素表示。
結(jié)論
慣性MEMS技術(shù)在過去幾年已經(jīng)取得長足進步,為系統(tǒng)開發(fā)商在復(fù)雜權(quán)衡范圍內(nèi)提供了廣泛的選項,包括尺寸、功耗、單位成本、集成成本和性能。對于首次利用MEMS IMU開發(fā)運動控制系統(tǒng)的人員,為了選擇合適的IMU并準備利用該IMU來支持關(guān)鍵系統(tǒng)需求,會有很多東西需要了解。對準精度對性能、成本和計劃方面的關(guān)鍵目標會有重大影響,必須予以認真考慮。在概念和架構(gòu)設(shè)計階段,即使很簡單的分析工具也能幫助找出潛在的風險,因此應(yīng)當趁著還有時間影響器件選擇、機械設(shè)計、安裝后校準(電子對準)、初步成本預(yù)測和關(guān)鍵計劃節(jié)點的時候,多做些工作。更進一步說,識別MEMS IMU的關(guān)鍵指標和機會,用系統(tǒng)中提供的自然運動代替三軸慣性測試設(shè)備以最大限度地發(fā)揮系統(tǒng)的價值(性能和總開發(fā)成本),將是非常有益的。
【推薦閱讀】






