【導(dǎo)讀】在分析Flyback電路之前,我覺(jué)得有必要把變壓器模型做一個(gè)總結(jié)���,因?yàn)槲覀儗?duì)變壓器的分析其實(shí)是在一定的模型上面進(jìn)行分析的���。這里闡述我的一個(gè)觀點(diǎn)�, 如果說(shuō)實(shí)際測(cè)試和實(shí)驗(yàn)是非常重要的話,對(duì)分析對(duì)象有一個(gè)清晰的模型概念對(duì)電子工程師來(lái)說(shuō)是非常必要的�,建立的模型的目的完全是為了可以簡(jiǎn)化問(wèn)題����。
功率變壓器模型
在分析Flyback電路之前,我覺(jué)得有必要把變壓器模型做一個(gè)總結(jié)�,因?yàn)槲覀儗?duì)變壓器的分析其實(shí)是在一定的模型上面進(jìn)行分析的。這里闡述我的一個(gè)觀點(diǎn)���, 如果說(shuō)實(shí)際測(cè)試和實(shí)驗(yàn)是非常重要的話�,對(duì)分析對(duì)象有一個(gè)清晰的模型概念對(duì)電子工程師來(lái)說(shuō)是非常必要的�,建立的模型的目的完全是為了可以簡(jiǎn)化問(wèn)題。當(dāng)然建立了模型進(jìn)行分析����,可能和實(shí)際的測(cè)試結(jié)果有出入,每一個(gè)對(duì)象的實(shí)際總有偏差�,但大規(guī)模生產(chǎn)有個(gè)前提就是需要控制對(duì)象的參數(shù)分布在一定范圍內(nèi)�����。
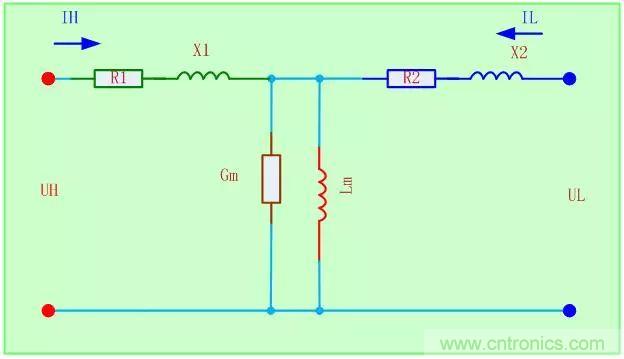
功率變壓器在電源中起著能量變換和能量傳送的作用(聯(lián)接信號(hào)源與負(fù)載的中介)���。一般的變壓器模型是一個(gè)雙端口網(wǎng)絡(luò),在大部分仿真軟件中的模型如下:
不過(guò)因?yàn)殡p端口模型不利于我們的分析�,我們一般不直接使用這種模型。(當(dāng)然軟件中大部分都是這么分析)這種模型忽略了漏磁電感和激磁電抗�����,需要進(jìn)行改進(jìn)才能得出比較精確的結(jié)果�����。
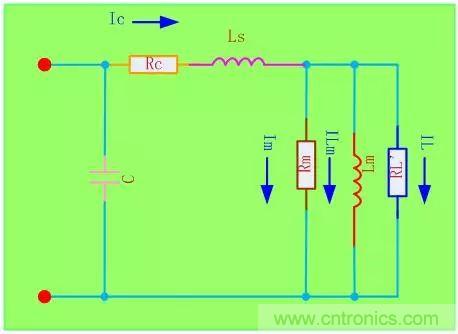
我們也可以將變壓器與負(fù)載分開(獨(dú)立的器件), 變壓器則等效成為附加一定電抗的電感器, 次邊電磁參數(shù)以一定變換歸一化到原邊進(jìn)行處理, 可看成一個(gè)單口網(wǎng)絡(luò)進(jìn)行等效, 從而使模型得以簡(jiǎn)化����。最簡(jiǎn)單的模型如下:
圖中各個(gè)參數(shù)為:
C:端口分布電容
Rc:線圈交流電阻
Rm:磁心損耗電阻
Ls:線圈漏感
Lm:磁心磁化電感
RL’:負(fù)載折合到原邊的等效電阻
主要缺點(diǎn)有兩個(gè):
1)I.c=I.m+I.lm+I.l,變壓器的銅損(線圈電阻損耗)與鐵損(磁芯損耗)是相關(guān)的,很難成為獨(dú)立的兩個(gè)參量���。
2)當(dāng)開關(guān)通斷的頻率比較高時(shí)�����,不同繞組間的電容效應(yīng)已較為明顯, 次邊繞組的銅損折合至原邊的等效阻抗已經(jīng)能夠明顯的影響變壓器的響應(yīng)�����。
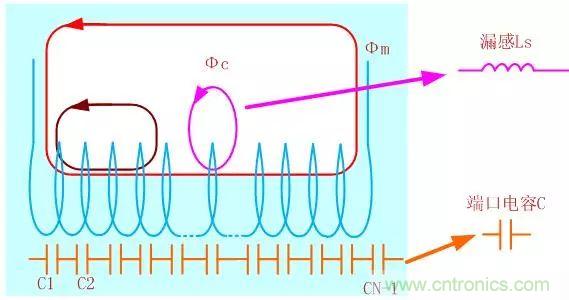
如果各位對(duì)上面的模型不太清楚���,以下這張圖能夠比較清晰的反應(yīng)變壓器線圈的分布參數(shù):
我們可以建立了一個(gè)繞組的模型����,端口電容也可以認(rèn)為是繞組的分布電容(匝間電容和層間電容)���,分布電容經(jīng)過(guò)疊加折算得:繞組的等效并聯(lián)電容C′= Ci/ ( N - 1) ( N > 1)Φm為主磁通(產(chǎn)生感應(yīng)電動(dòng)勢(shì))對(duì)應(yīng)磁芯磁化電感Lm,Φc為漏磁通對(duì)應(yīng)線圈漏感
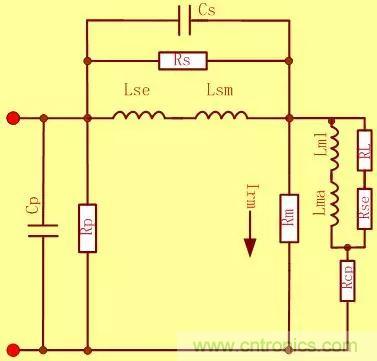
第一個(gè)改進(jìn)型模型:
Cp:端口并聯(lián)等效分布電容(初級(jí)線圈)
Rp:端口并聯(lián)等效介質(zhì)損耗電阻(次級(jí)線圈)
Cs:初級(jí)和次級(jí)繞組間等效耦合電容
Rs:初級(jí)和次級(jí)繞組間等效介質(zhì)漏
Ls:線圈漏電感����,分為L(zhǎng)se和Lsm
Lm:勵(lì)磁電感,分為L(zhǎng)ma和Lml
Rm:磁心損耗等效電阻
Rcp:原邊繞組的等效電阻
Rce:次邊繞組的等效電阻
RL:折算到原邊的負(fù)載等效電阻
模型主要特點(diǎn):
流過(guò)Rce的電流I.Rce ,流過(guò)Rcp的電流I.Rcp ,流過(guò)Rm的電流I.Rm 相互獨(dú)立, 模型使源邊副邊的銅損與磁芯損耗(鐵損)不再相關(guān)。
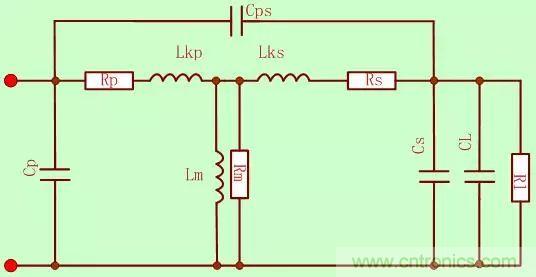
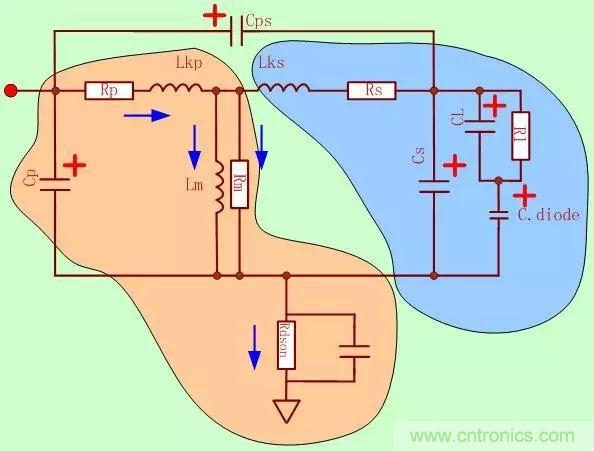
不過(guò)個(gè)人認(rèn)為下面這個(gè)模型更好理解一些:
Cps為初級(jí)和次級(jí)繞組之間的電容
Lkp:初級(jí)繞的漏感
Cp:初級(jí)繞組的寄生電容(分布電容)
Rp:初級(jí)繞組的線圈電阻
Lks:次級(jí)繞的漏感
Cs:次級(jí)繞組的寄生電容(分布電容)
Rs:次級(jí)繞組的線圈電阻
Lm:變壓器勵(lì)磁電感
Rm:磁芯損耗的電阻
RL:折算到原邊的負(fù)載等效電阻
CL:折算到原邊的負(fù)載等效電容
這個(gè)模型可能好理解一些���,不過(guò)我們分析的時(shí)候可以從這些模型開始參照���,或者說(shuō)分析的時(shí)候通過(guò)某些參數(shù)的變化來(lái)分析整個(gè)趨勢(shì)。
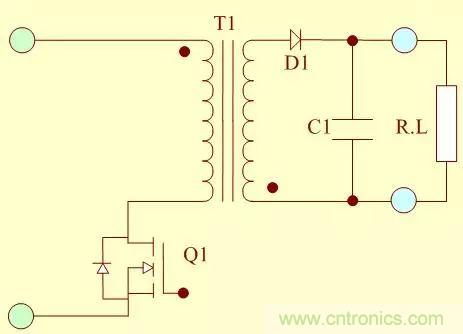
激式電源的開關(guān)過(guò)程分析
關(guān)于這個(gè)論題很多人已經(jīng)給出了它們的分析����,不過(guò)呢寥寥幾句有時(shí)候帶給人更多的是疑惑和迷茫����。參考了一些論文和分析�����,把我個(gè)人對(duì)這個(gè)問(wèn)題的分析表述出來(lái)�,可 能和設(shè)計(jì)的分析會(huì)有一些誤差,不過(guò)提出一個(gè)大家看得懂的問(wèn)題總是比努力去看懂一些生澀的文字要好些(這里說(shuō)明一點(diǎn)�,做的分析和示意可能并不是對(duì)的)。
我們分析的主要問(wèn)題還是在Q1管子在關(guān)斷過(guò)程中的響應(yīng)���,至于設(shè)計(jì)電路減小這個(gè)響應(yīng)的影響�,方法有很多���,個(gè)人以為就取值和影響合在一起做一個(gè)小專題�����。
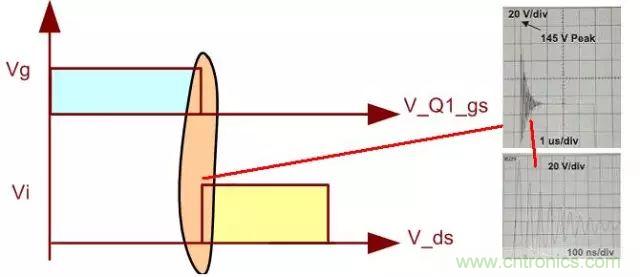
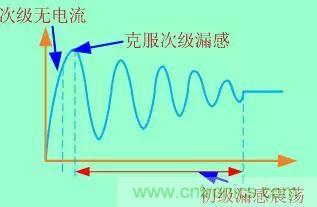
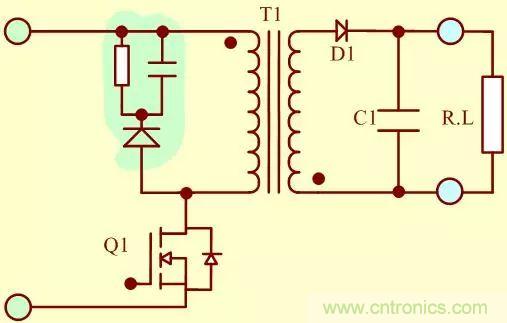
在關(guān)斷過(guò)程中�����,如果不考慮加入抑制暫態(tài)過(guò)程的電路����,我們看到的波形將不會(huì)是理想的,如下圖所示:
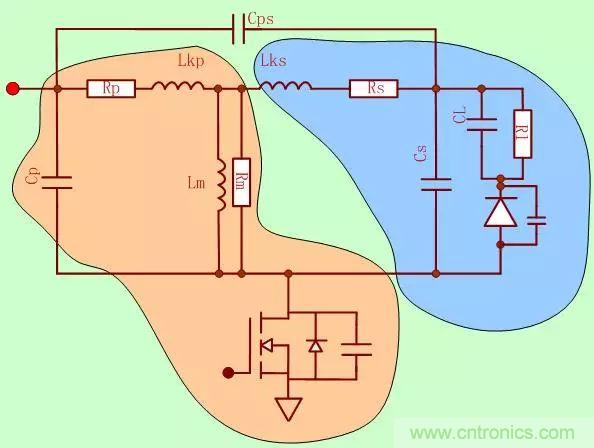
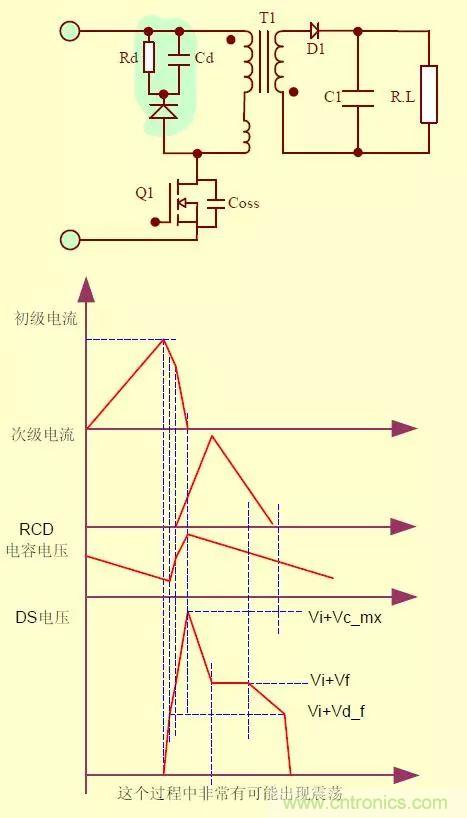
把上面的功率變壓器模型改進(jìn)模型2帶入其中分析:
Mos管關(guān)斷前的穩(wěn)態(tài)分析:
勵(lì)磁電感和漏電感中均儲(chǔ)存能量����,同時(shí)由于二極管的結(jié)電容存在,次級(jí)電容上都存在一定的電壓���,次級(jí)漏感中無(wú)電流�。
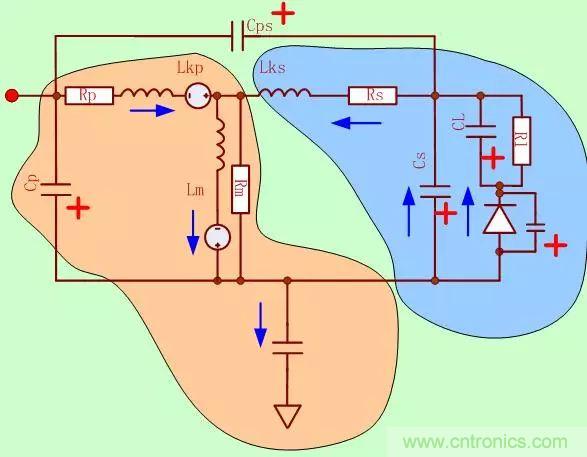
然后我們把Mos管關(guān)掉�,看下圖:
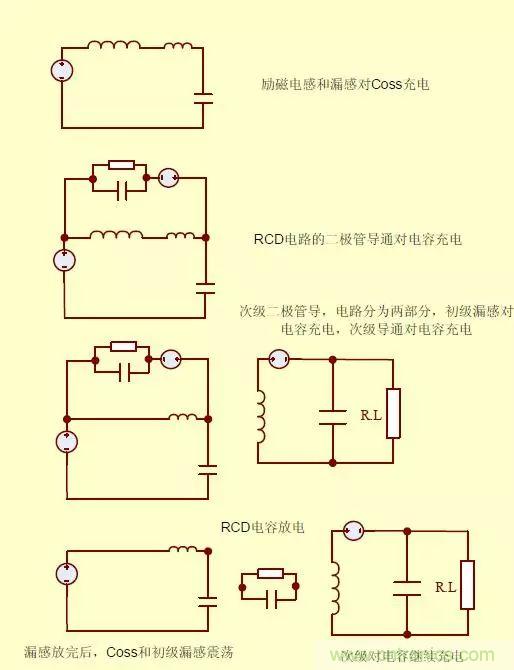
我們來(lái)吧上面的過(guò)程整理一下:
1.MOS管關(guān)斷后,初級(jí)電流(勵(lì)磁電感和初級(jí)漏電感和電源的綜合作用)給MOS輸 出電容充電,初級(jí)電容���,初次級(jí)之間電容,次級(jí)電容�,次級(jí)二極管電容,負(fù)載電容則開始放電(你可以這樣理解�����,因?yàn)閴翰钚×耍娙莘烹?��,也可以理解為反向?電)�����,Mos管DS端電壓是上升的(這里可以認(rèn)為是上面所涉及的分布參數(shù)之間的諧振�,這個(gè)電路的Q之很小的)�����,此時(shí)的電壓可以認(rèn)為是線性上升的�����。注意此時(shí)的次級(jí)的二極管是沒(méi)有導(dǎo)通的�����,因?yàn)镈S端電壓比較小�����。
2.當(dāng)DS端電壓上升�,次級(jí)的電壓達(dá)到輸出電壓(這是客觀存在的����,因?yàn)槲覀円WC輸出電壓的穩(wěn)定)+整流管的電壓后,如果沒(méi)有次級(jí)漏感����,次級(jí)回路就導(dǎo)通了,因此DS端電壓會(huì)繼續(xù)上升�,當(dāng)克服了次級(jí)漏感的影響后,次級(jí)電流開始上升���,在這個(gè)時(shí)候勵(lì)磁電感的能量由于有更小的阻抗通路�,從初級(jí)來(lái)看�����,初級(jí)電流會(huì)減小���。
3.這個(gè)時(shí)候起決定性作用的就變成了初級(jí)漏感���,它不能耦合到次級(jí)上沒(méi)有小的阻抗通路����,因此初級(jí)漏電感就和Mos管輸出電容之間和初級(jí)電容之間諧振,電壓形成幾個(gè)震蕩(如果沒(méi)有吸收和clamped電路這個(gè)過(guò)程會(huì)持續(xù)很久)。
初級(jí)漏感電流是初級(jí)電流的一部分���,因此伴隨著初級(jí)漏感電流的下降的是次級(jí)電流的上升����,如果沒(méi)有clamped電路����,電流的下降會(huì)非常快����,如果加入clamped電路等于把這個(gè)過(guò)程拉長(zhǎng),電壓應(yīng)力也就減小了���。
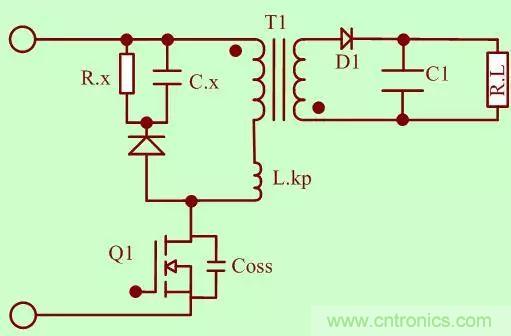
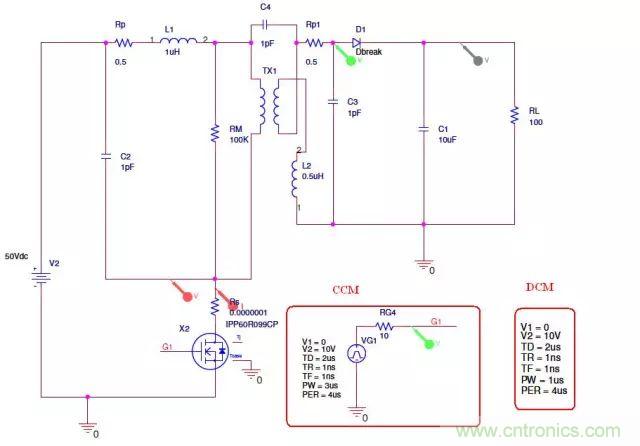
反激DCM模式RCD參數(shù)計(jì)算
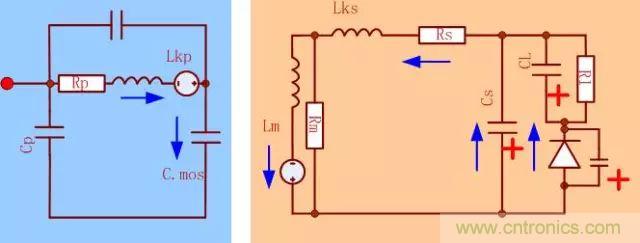
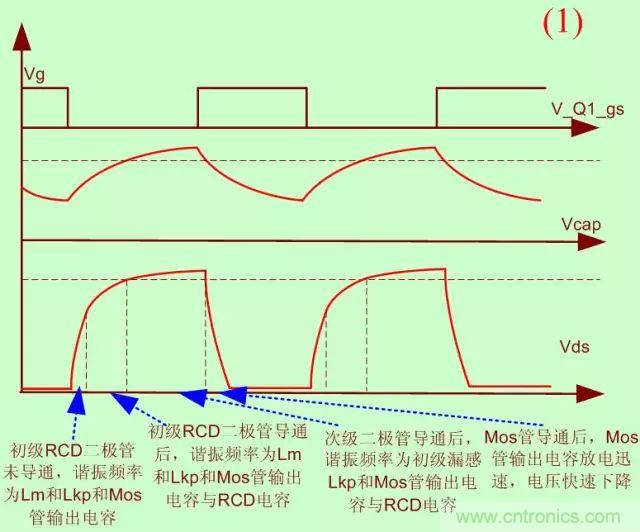
首先我們將關(guān)心的因素縮小�,把主要考慮的元素分為Mos管的等效輸出電容Coss���,變壓器勵(lì)磁電感Lm�,變壓器的初級(jí)漏感Lkp作為考慮對(duì)象����。
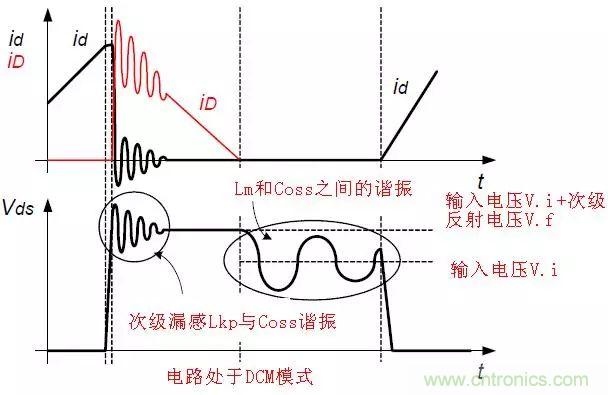
如圖所示����,如果不加RCD鉗位�����,電路在DCM模式下�,電路可能發(fā)生兩次振蕩,第一次主要是初級(jí)漏感Lkp和Coss的電容引起的���,第二次主要是在電路能量耗盡后�,勵(lì)磁電感和Coss電容振蕩引起的這里需要補(bǔ)充一下�����,在仿真的時(shí)候�,已經(jīng)觀察到了這個(gè)明顯的現(xiàn)象了。
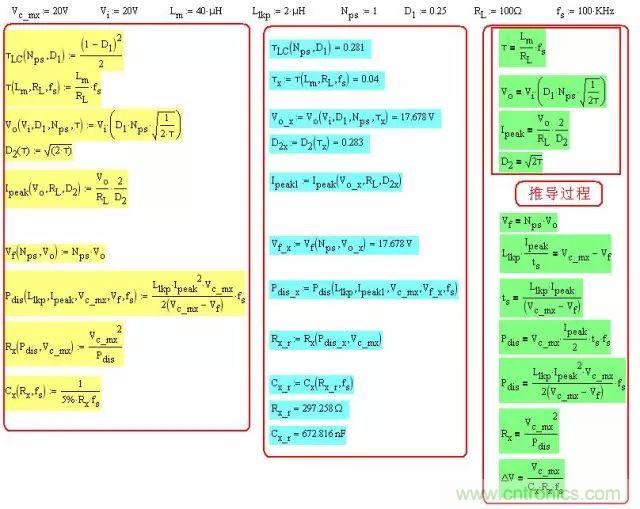
下面開始我們的計(jì)算:
計(jì)算過(guò)程�,把Flyback的計(jì)算過(guò)程帶入其中:
找了好些文檔都是這么計(jì)算的,不過(guò)我發(fā)現(xiàn)幾個(gè)問(wèn)題
1.消耗的能量不僅僅是漏感的�����,也包括勵(lì)磁電感的能量
2.在鉗位過(guò)程中�,電壓是變化的,并不存在徹底鉗位在V.c_mx的情況發(fā)生
因此我們需要修改模型
RCD吸收電路的影響和設(shè)計(jì)方法(定性分析)
介紹RCD電路的影響����。
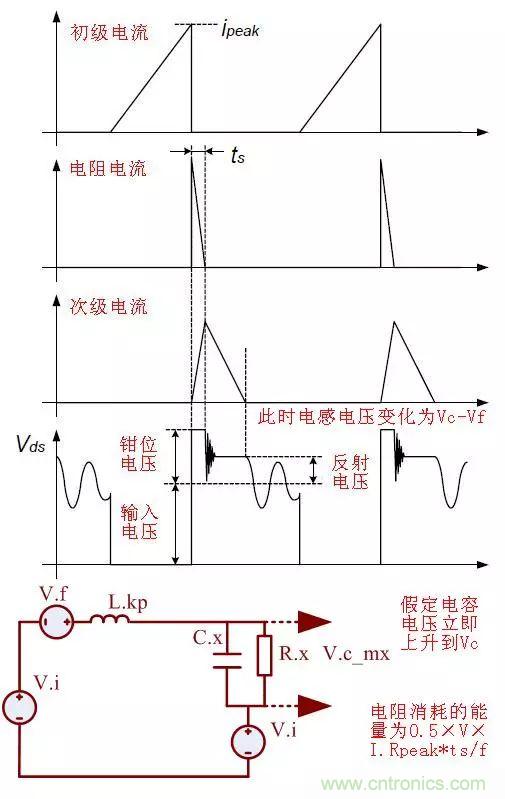
先分析過(guò)程:
對(duì)應(yīng)電路模型:
我們可以定性的分析一下電路參數(shù)的選擇對(duì)電路的暫態(tài)響應(yīng)的影響:
1.RCD電容C偏大
電容端電壓上升很慢,因此導(dǎo)致mos 管電壓上升較慢����,導(dǎo)致mos管關(guān)斷至次級(jí)導(dǎo)通的間隔時(shí)間過(guò)長(zhǎng),變壓器能量傳遞過(guò)程較慢�,相當(dāng)一部分初級(jí)勵(lì)磁電感能量消耗在RC電路上 。
波形分析為:
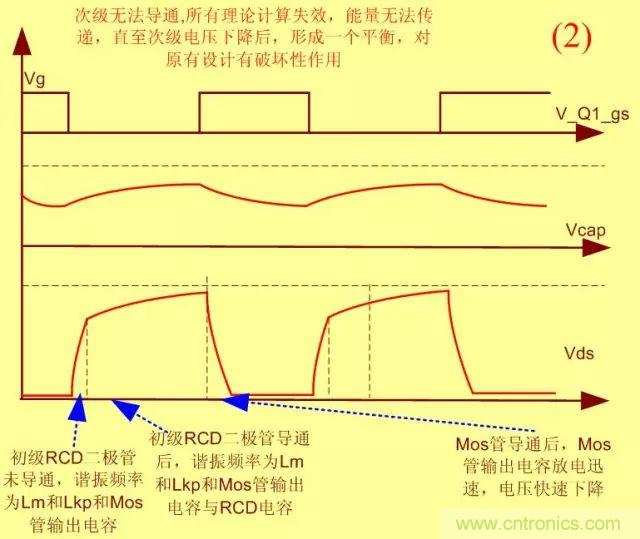
2.RCD電容C特別大(導(dǎo)致電壓無(wú)法上升至次級(jí)反射電壓)
電容電壓很小�,電壓峰值小于次級(jí)的反射電壓,因此次級(jí)不能導(dǎo)通�����,導(dǎo)致初級(jí)能量全部消耗在RCD電路中的電阻上���,因此次級(jí)電壓下降后達(dá)成新的平衡�,理論計(jì)算無(wú)效了����,輸出電壓降低。
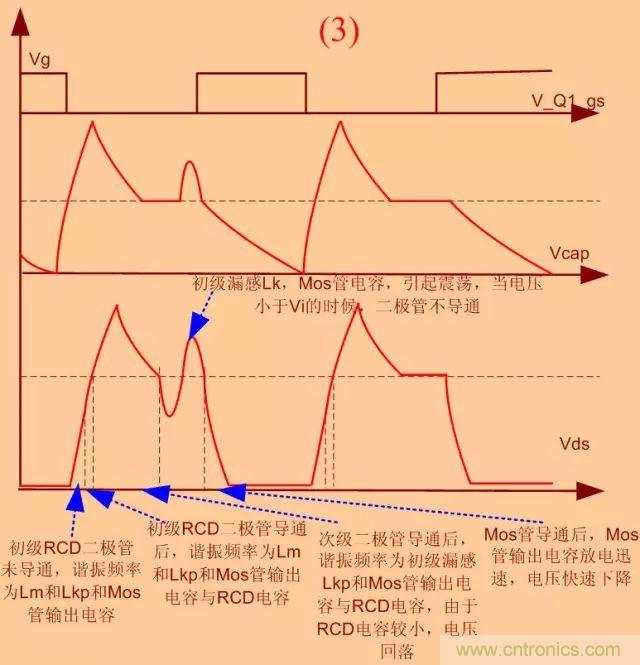
3.RCD電阻電容乘積R×C偏小
電壓上沖后�,電容上儲(chǔ)存的能量很小���,因此電壓很快下降至次級(jí)反射電壓,電阻將消耗初級(jí)勵(lì)磁電感能量�����,直至mos管開通后���,電阻才緩慢釋放電容能量�����,由于RC較小���,因此可能出現(xiàn)震蕩,就像沒(méi)有加RCD電路一樣�����。
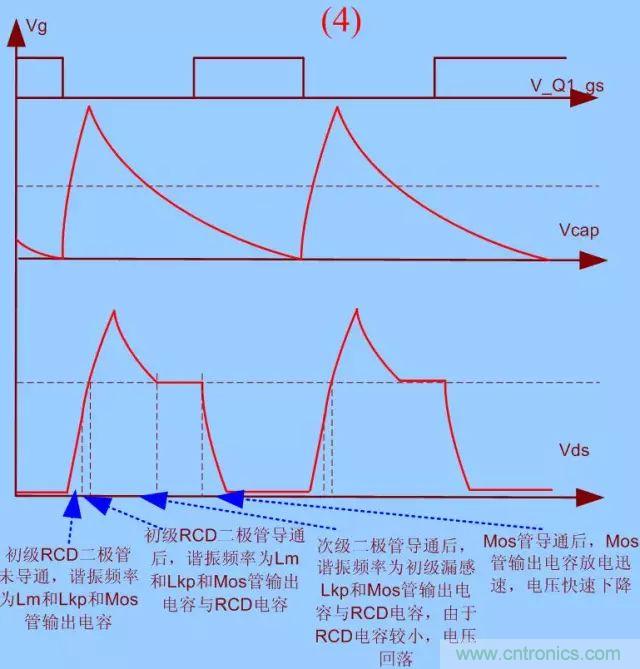
4.RCD電阻電容乘積R×C合理���,C偏小
如果參數(shù)選擇合理�����,mos管開通前�����,電容上的電壓接近次級(jí)反射電壓�����,此時(shí)電容能量泄放完畢�,缺點(diǎn)是此時(shí)電壓尖峰比較高�,電容和mos管應(yīng)力都很大
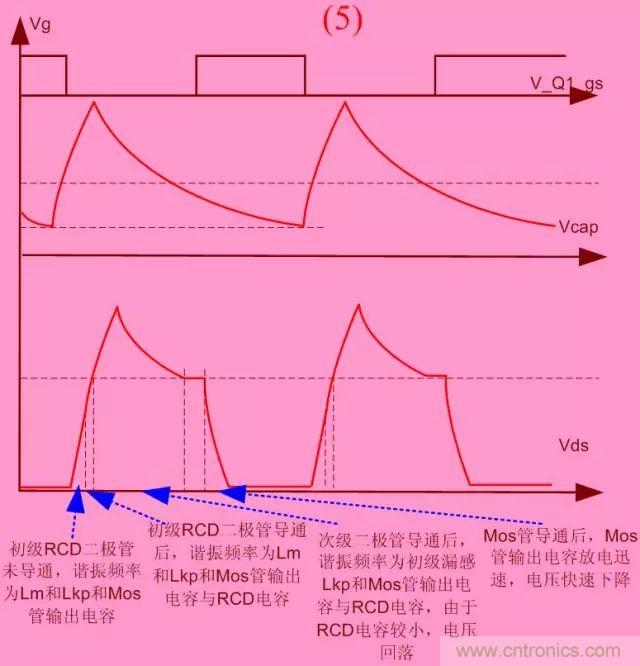
5.RCD電阻電容乘積R×C合理,R���,C都合適
在上面的情況下����,加大電容�,可以降低電壓峰值,調(diào)節(jié)電阻后����,使mos管開通之前,電容始終在釋放能量�,與上面的最大不同���,還是在于讓電容始終存有一定的能量。
以上均為定性分析�����,實(shí)際計(jì)算還是單獨(dú)探討后整理�,需要做仿真驗(yàn)證。
反激開關(guān)過(guò)程和RCD電路的影響(仿真結(jié)果)
下面做了一些仿真�����,果然和上面的文章分析的相互印證
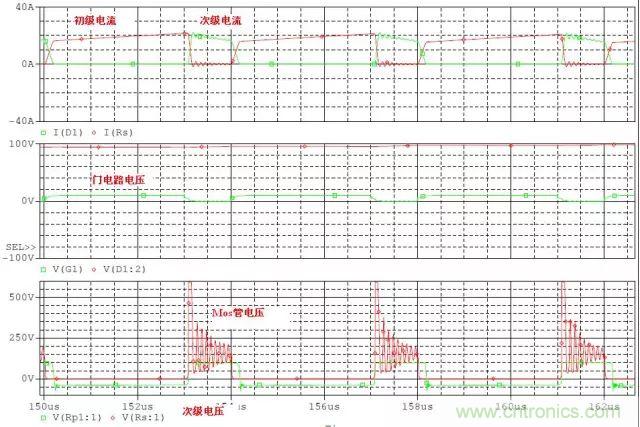
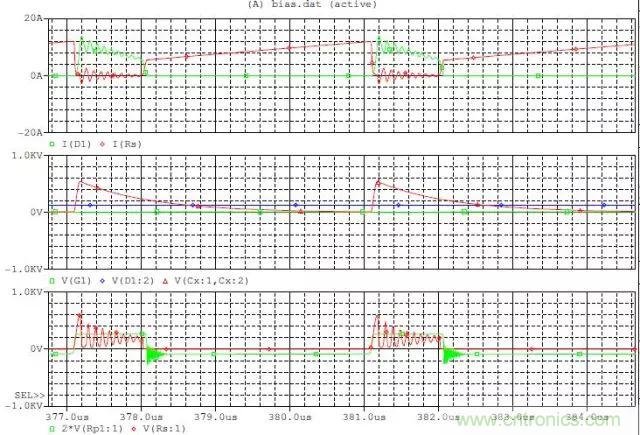
先看看無(wú)RCD電路的情況:
CCM的電路:
Duty cylce=0.75
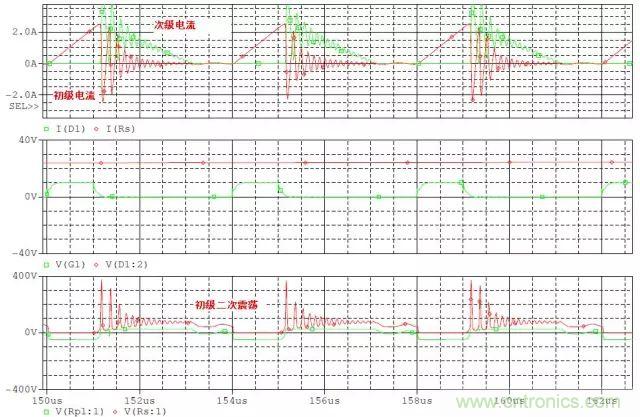
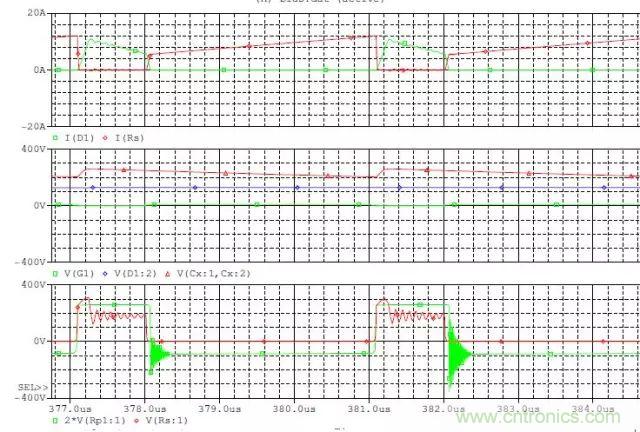
DCM的電路:
Duty cylce=0.25
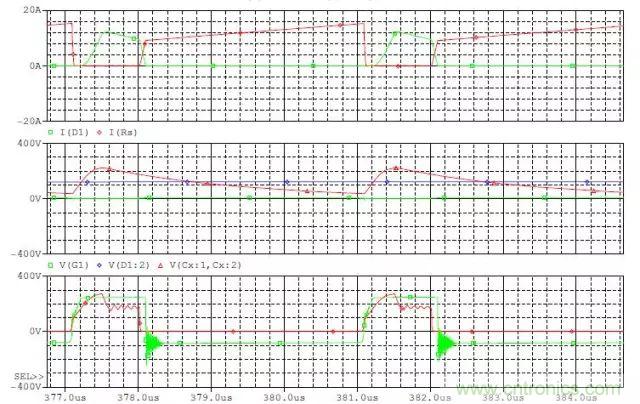
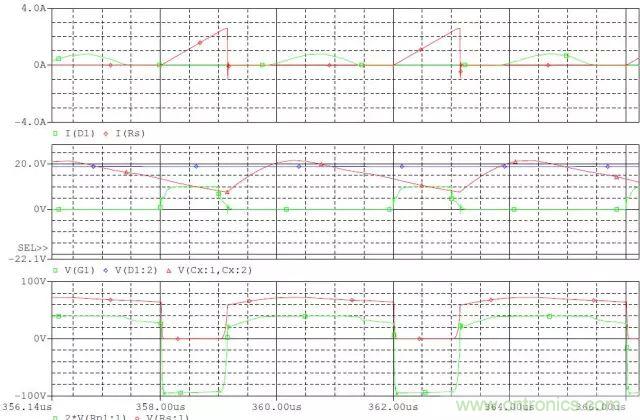
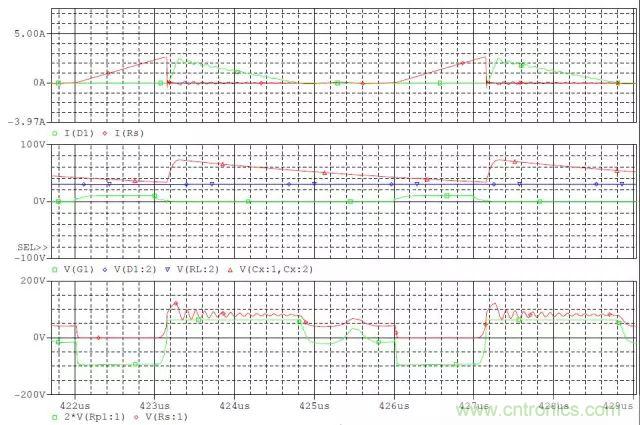
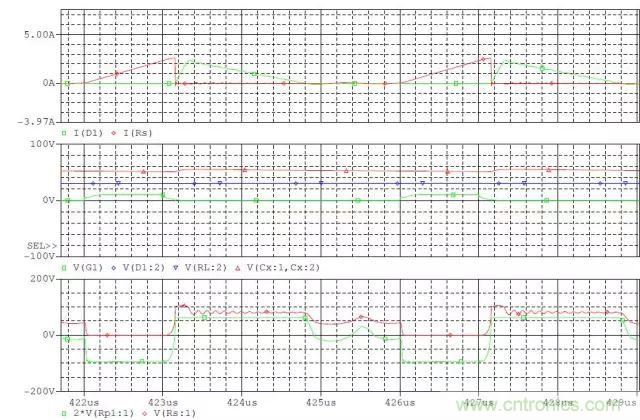
CCM補(bǔ)償RCD電路后電壓和電流波形
1) C較大
2) RC過(guò)小
3) RC合適
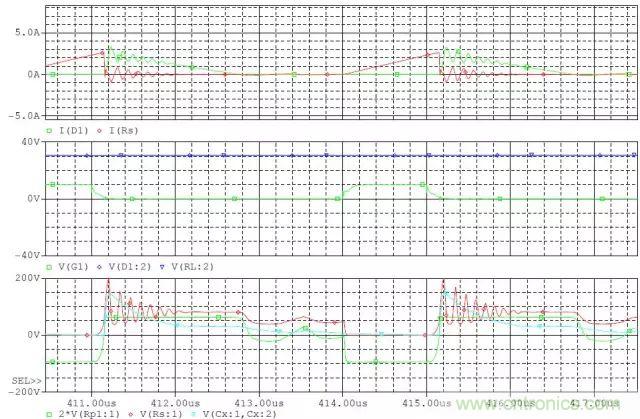
DCM補(bǔ)償RCD電路后電壓和電流波形
1) C過(guò)大(R=20,C=50nF)
從圖上看�����,對(duì)輸出影響確實(shí)很大�����。
2) RC過(guò)小
3) RC合適���,C略小
4)RC合適����,C略大
推薦閱讀: